So you're making an RSA key for an HTTPS certificate. What key size do you use?

So you're about to make an RSA key for an SSL certificate. What key size should you use?

• OpenSSL now use a 2048 bit key by default.
• Windows certreq makes you explicitly specify a key size and uses 2048 bit examples in its documentation
• If you want to show the verified company name in the green bar in a browser, you'll need an EV certificate, which requires a 2048 bit RSA key at minimum.

Since CertSimple only do EV certificates, we use a 2048 bit key in the bash & powershell we generate during our application process.

But why not go further? What experts have to say about 4096 bit keys varies greatly:

• Most software development websites - GitHub, Stripe, npm, and Mozilla - use 2048 bit EV certificates at present.
• GnuPG thinks 4096 bit keys are unnecessary.
• But SSL Labs requires a 4096 bit key to get a 100% score for Key Exchange.

You're probably already aware that with a 4096 bit key:

• There's an increase in encryption strength.
• The SSL handshake at the start of each connection will be slower.
• There's an increase in CPU usage during handshakes.

But you may not be sure of the extent of each of these these effects. So: let's measure all these things.

Measuring encryption strength

Unlike traditional symmetric algos, asymettric algos like RSA (unfortunately) don't double in strength when you add a single bit.

So RSA key sizes are evaluated by National Institute of Standards and Technology by converting them to equivalent symmetric cipher values (see 'Comparable Algorithm Strengths'). NIST tells us a 2048 bit RSA key is equivalent to a 112 bit symmetric cipher.

NIST says a 2048 bit RSA key has a strength of 112 bits: i.e., there are theoretically 2¹¹² possibilities to crack the private key.

Calculating RSA strength yourself

The NIST says they're using 'currently known methods' to build their data, but some clever folk on Crypto Stack Exchange worked out that the NIST data appears to use an algorthm to calculate the complexity of using a factoring attack called the 'number field sieve' by Dutch cryptographer Arjen K. Lenstra. This is handy, since the NIST recommendation doesn't include every key size. If you felt like firing up Mathematica, we could get results for, eg, a 2048 bit RSA key with:

> N[Log2[Exp[(64/9*Log[2^2048])^(1/3)*(Log[Log[2^2048]])^(2/3)]]]
116.884

The Mathemetica code above was ported from Reid Wiggins' code on Crypto Stack Exchange - cheers Reid!

Since not everyone has Mathematica we ported the GNFS complexity calculator to node.js:

var getRSAStrength = require('ssl-rsa-strength');
getRSAStrength(2048);

You can use this to measure RSA strength in node.js or any web browser and also to test key sizes not included in NIST's report. The results show a 2048 bit RSA key is equivalent to around 116 'bits' of a symmetric algo. Actually, 116.884, but since, you can't have .884 of a bit our JS implementation rounds down.

Note that NIST also round the GNFS complexity's result down to 112 bits, a common symmetric cipher size, to allow people to apply the same policies they would if they were considering symmetric algorithms. Our JS and the Mathemetica code above give the raw GNFS complexity.

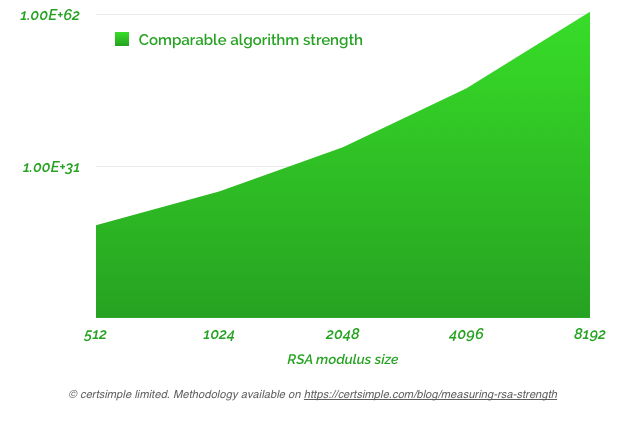
Strength for common key sizes using GNFS complexity, logarithmic scale.

Note: as mentioned in the tool's README:

The GNFS complexity measurement is a heuristic: it's a tool to help you measure the relative strengths of different RSA key sizes but it is not exact. Implementation details, future vulnerabilities in RSA, and other factors can affect the strength of an RSA key. The attack that breaks RSA 2048 could also break RSA 4096.

Notwithstanding these limitations, GNFS complexity is the best way to measure the raw strength of asymmetric encryption algorithms like RSA.

Measuring the increased load on the server

Bigger RSA key sizes may slow down handshaking from the users point of view. On a Mac or Linux machine you can get some time taken to sign a 2048 bit RSA vs 4096 bit RSA with the openssl speed rsa command:

                  sign    verify    sign/s verify/s
rsa  512 bits 0.000210s 0.000014s   4772.1  69667.5
rsa 1024 bits 0.000727s 0.000035s   1375.3  28508.9
rsa 2048 bits 0.003778s 0.000092s    264.7  10899.5
rsa 4096 bits 0.022637s 0.000305s     44.2   3275.4

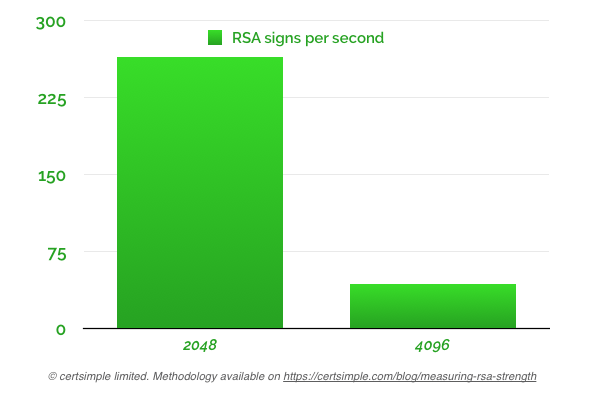
Looking at the results, it's pretty clear:

4096 bit handshakes are indeed significantly slower in terms of CPU usage than 2048 bit handshakes.

Keep in mind handshakes are brief: after key exchange with RSA, the browser and server have agreed on session key, and a fast symmetric encryption algo like AES is used.

Measuring browser handshakes

We can also do a more practical test by reconfiguring a webserver with 2048 and 4096 bits keys and then measuring the SSL handshake time in Chrome:

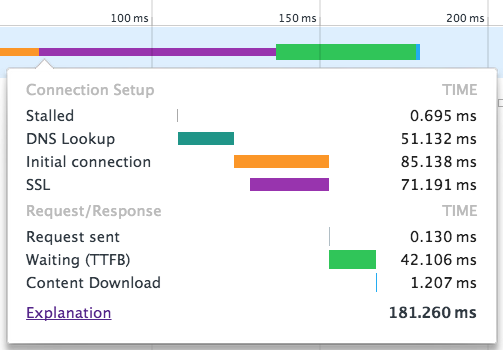
Running 5 test each on both key sizes, with the browser process restarted in between, returned:

• An average handshake of 50ms with a 2048 bit RSA key
• An average handshake of 76ms with a 4096 bit RSA key

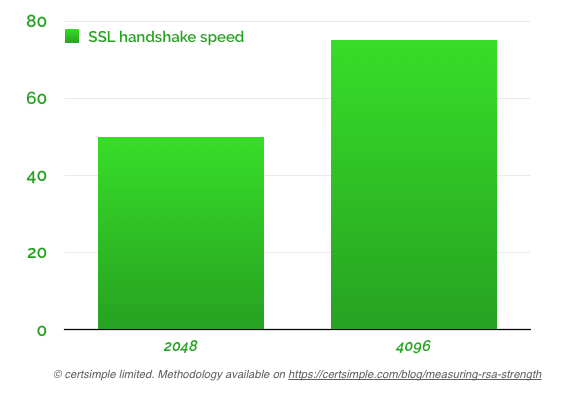
The added latency of the 4096 bit key was definitely noticeable, but handshaking was still quite fast.

Google want most pages to load within 100ms, Amazon find that every additional 100ms causes a drop in sales. Handshakes block everything - if your site is set up correctly, everything will be loaded by HTTPS and not a single resource will start loading until the handshake is complete.

But whether 25ms - 25/1000ths of a second is an issue depends on your site. Many websites - including ours - have a lot of optimisation to do before handshake latency becomes an issue.

We will run this test on a less powerful mobile device in future.

4096 bit compatibility concerns

AWS users should also keep in mind Amazon CloudFront also only support 2048 bit keys. Cisco IOS XE prior to Release 2.4 and Cisco IOS Release 15.1(1)T do not support 4096 bit keys

Summary

So... what do we think:

Per the introduction, you should definitely pick at least a 2048 bit key: the makers of openssl, Microsoft, and every web browser are pushing you to use a 2048 bit key at minimum.

Should you use 4096 bit keys? Let's consider our results:

• A 4096 bit key does provide a reasonable increase in strength over a 2048 bit key, and according to the GNFS complexity, encryption strength doesn't drop off after 2048 bits.
• There's a significant increase in CPU usage for the brief time of handshaking as a result of a 4096 bit key
• There's a small increase in browser response for the brief time of handshaking as a result of a 4096 bit key

You can replicate the results of the above tests easily and should do so.

There's no hard answer here but some points:

• Your server and openssl version is different to the one used in testing, and as time goes on, browsers march forward. Run your own tests and get your own results.
• Consider other factors beyond strength and performance: there may be other attacks against RSA that come into play by the time you make a decision. As we've seen elsewhere, bit length isn't the only aspect to how secure a given implementation is
• Keep in mind an EV cert on your web server lasts two years before you need to get re-verified. If for some reason you want to change your bit length before it expires, you can re-key your certificate for free - some SSL vendors charge for this, but we don't.

OK, but what will we, CertSimple, do?

• Are we going to re-key our own certificate to 4096 bit?
• Should we change the bash/powershell CertSimple generates to be 4096 bits by default?

No. We can re-key pretty quickly, so deploying a 4096 bit key would be pretty easy, but we feel like a 2048 bit key provides a reasonable speed/security/compatibility tradeoff - as we might move to AWS in future, the last one is also a concern for us.

On the other hand, what do we think about using a 4096 bit key? Is 4096 bit RSA horrible and slow? No. Looking at the results, the server CPU use and additional latency could be reasonable for some sites that desire the gain in strength.

Note: a previous version of the article mentioned 'there are theoretically 2^112 possibilities to brute force the private key' - this was incorrect. There are theoretically 2^112 possibilities to crack the private key using techniques other than brute force. Thanks to dchest on Hacker News for pointing out the error.